Scientists have long been fascinated by how tissues heal, and much of this research has focused on the epithelial layer—a thin, protective layer of cells that forms the outer surface of tissues. In their studies, researchers have looked at this layer across a range of organisms, from the wing of the fruit fly to the outer layers of jellyfish, as well as lab-grown kidney epithelial cells. These models give us insight into how tissues repair themselves after injury. While many studies have explored the integrated mechanisms of wound healing, such as tissue proliferation, both through computational and experimental approaches, the material properties of epithelial tissue and their role in healing have received less attention.
A recent study has uncovered a surprising insight into the mechanics of wound healing: the closure of wounds is subject to geometric limitations in the absence of tissue proliferation. In other words, no matter how large or small the wound, there are certain physical properties of tissues that set boundaries on how much the wound can heal. Researchers from NCBS and IIT Bombay have developed a mathematical model that can predict the fate of a wound based on its geometrical features and the tissue’s mechanical properties. The team reports that based on the size of the wound in an epithelial monolayer, actin-myosin contractility and cell-cell adhesion can guide if the wound shrinks or ruptures the tissue further.
“We introduce here a mathematical model that incorporates different forces involved in the process of wound healing. The mathematical model helps us to find how these forces compete and cooperate with each other and a wound will ultimately close or not”, says Sayantan Dutta, senior author of the study and assistant professor, IIT Bombay.
Their research findings highlight that in the absence of cell death and cell division, there is an extent to which a wound can close. This limit is dictated by the geometry and mechanical properties of the tissue itself, such as its size, elasticity, and the forces at play during the healing process. Their analysis reveals that some wounds will never fully close, even if they start small. Instead, these wounds reach a point where healing stops, governed by a fixed upper limit. Using an experimental setup of monolayers of kidney epithelial cells (MDCK), they replicate the physical scenario depicted in the model.
The parameters used in the mathematical model represent the elasticity of the tissue, size of the tissue, tissue fluidity, tension at the tissue-wound boundary, size of the tissue and size of the wound, says Nandhu Krishna Babu, lead author of the study.
They also show that for very large tissues, all wounds end up having the same final wound fraction irrespective of the value of the initial wound fraction.
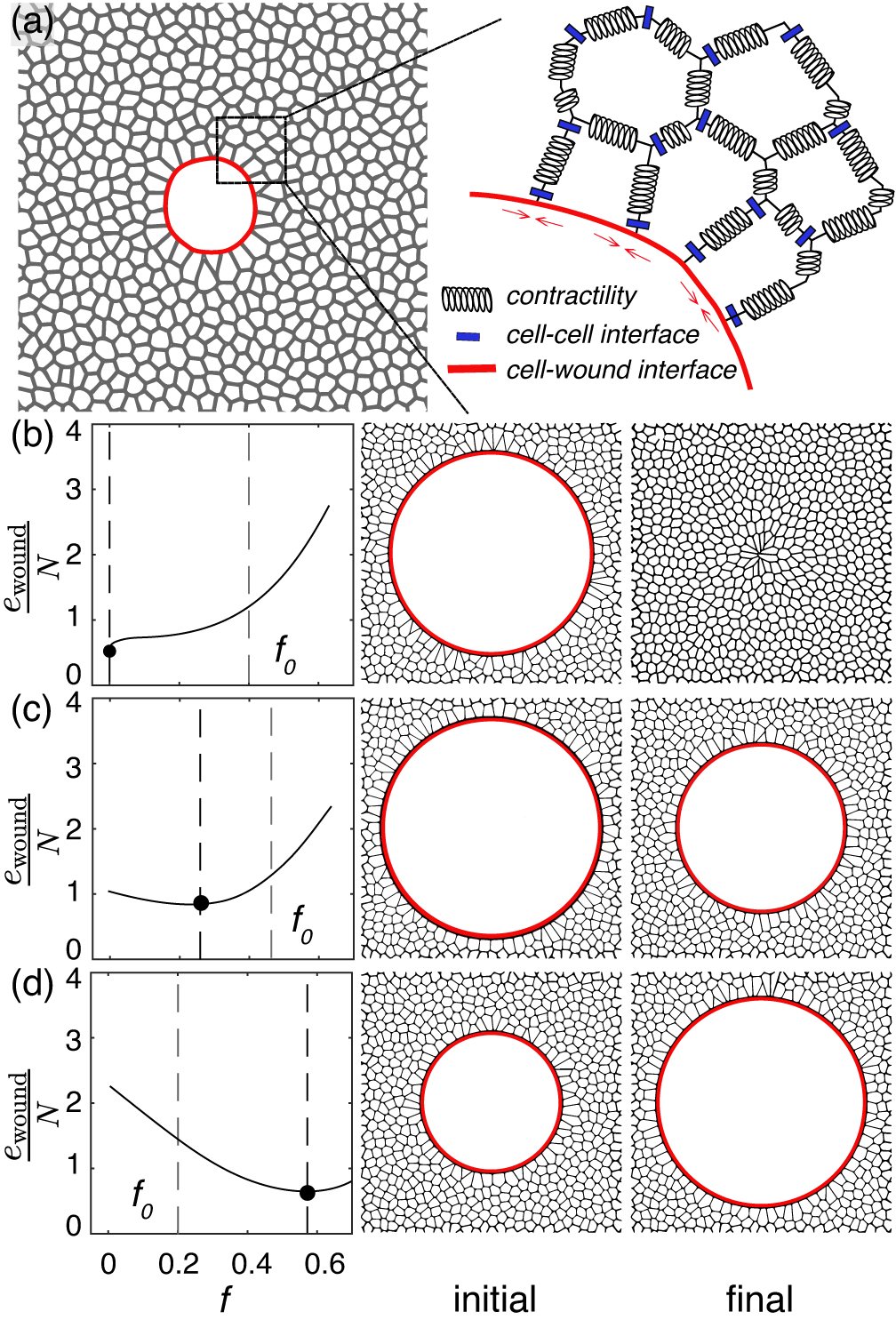
“For wounds which shrink but don't close, irrespective of the tissue size, they all end up having the same final wound fraction. This is because the system has an energy minimum at the same final steady-state wound fraction irrespective of its size”, Nandhu.
To validate these theoretical findings, the research team employed MDCK monolayers in their experiments. They found that, within tissues of the same size, wounds with a higher initial area fraction fail to close, while wounds with the same area fraction do not close in larger tissues. Furthermore, their theoretical model, based on the mechanical parameters of living tissues, robustly predicts the experimental observations. Additionally, the wound states predicted by their theory show strong quantitative agreement with their experimental results.
"Examining wound healing in an epithelial monolayer allowed us to independently control the tissue size and the wound size", says, Tapomoy Bhattacharjee, senior author of the study and assistant professor, NCBS.
These findings shed light on the underlying mechanics that govern the healing process, offering a new perspective on how our bodies recover from injury.









0 Comments